グリコ、チヨコレイト、パイナツプル
穂滝薫理
序.ジャンケン必勝法
私の友人の片田君によると、ジャンケンには必勝法があるという。正確には、必ず勝つ方法ではなくて、“勝つ確率が最も高くなる方法(手の出し方)”である。それは“グー、チョキ、パーを3分の1ずつの頻度でランダムに出す”というものだ。なんか拍子抜けするような必勝法だが、この方法なら、勝つ確率は、当然3分の1(約33.3%)となり、そしてジャンケンではそれが“最も高い勝つ確率”なのだそうだ。
ただし、これには条件がつく。それは、(1)相手の戦略が不明のとき、(2)十分な勝負数が得られるとき、の2つ。(1)は、もし相手の戦略がわかっているなら、それに対応した手を出したほうが勝つ確率は高い。たとえば、相手が“グーしか出さない”という戦略を取ることがわかっているなら、こちらは“パーしか出さない”という戦略を取れば、勝つ確率は当然33.3%よりも高くなる。というかこの場合の勝つ確率は100%で、まさに必勝法となる。また、たとえば、“グー、チョキー、パーをこの順番で繰り返して出す”という戦略を相手が取っているなら、こちらが取るべき戦略は言うまでもないだろう。片田君の必勝法は、そのような相手の戦略がわからないときでも、最大の勝率33.3%を得られるというものだ。逆に言うと、“たとえ相手がどんな戦略を取っている場合でも”、最も勝つ確率の高い戦略なのだ。また、(2)について、この必勝法が、一発勝負や、三本勝負で二本先取勝ち、というような勝負には当てはまらないことを表わしている。確率の話なのだから、当然と言えるだろう。たとえコインの表が出る確率が50%だからって、2回投げたら必ず表と裏が1回ずつ出るわけではないのと同じことだ。つまり、片田君の必勝法は、100回、1000回と十分な勝負数が得られるときに、33回なり333回なり、33.3%に近い回数勝てるということである。
続いて片田君は「何て呼ぶのか知らないけれど、ジャンケンをして、グーで勝ったら“グリコ”で3歩、チョキで勝ったら“チヨコレイト”で6歩、パーなら“パイナツプル”で6歩と、その文字数だけ進んだり階段を登れるって遊びがあるじゃない? あれの必勝法(勝つ確率が一番高い手の出し方)もあるんだ」ということを岡山弁で言った。だが、ついにその方法は教えてくれなかった。
そこで、本論文は、そいつを独自に調査・検証してみるものである。
1.ジャンケンの勝負マトリックス
|
|
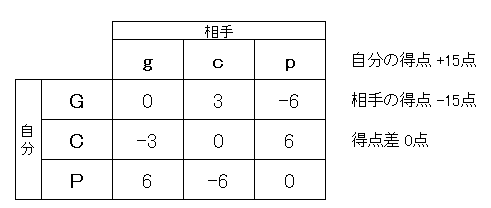
普通にジャンケンを行なったとき、起こりうる勝負結果を図1“ジャンケンの勝負マトリックス”に示す。ジャンケンでは、相手も自分も出しうる手は3通りで、その結果は3×3=9で9通りとなる。そのうち、“勝ち”となるのは3通りで、勝つ確率は3÷9=0.33333…となり、確かに約33.3%である。しかし、よく考えてみると、“負け”となるのも同様に3通り、つまり約33.3%で、実は片田君の必勝法は、自分も相手も勝つ確率がいっしょという対等な勝負であることがわかる。と同時に、ジャンケン勝負の透明性というか、自分も相手もどちらも最初から有利も不利もないという公平さもわかる。グリコ、チヨコレイト、パイナツプルによるジャンケン(めんどくさいので以後“グリコケン”と呼ぶ)は、自分と相手の出した手により、たんに勝ち負けだけでなく結果に点数すなわち重みをつけたものである。そのマトリックスを図2に示す。ただし、ここでは、グー、チョキ、パーを、自分の手なら大文字でG、C、P、相手の手なら小文字でg、c、pと置いてある。また、得点(進める歩数に該当する)は、自分の勝ちならプラス、相手の勝ちならマイナスで表わしてある。すなわち、自分がグーで相手がパーを出したときは、“Gp”の欄を見ると“-6”となっていて相手が6歩進めることがわかる。
|
|
さて、図2を見ると、9通りの試合結果で、自分が得ることのできる総得点は15点、相手の総得点も15点(図2ではー15点)となり、普通のジャンケンと同様に対等の勝負であるように見える。はたして本当にグリコケンの必勝法なんてものがあるのだろうか?
ところで片田君はこのグリコケンの必勝法についてヒントを教えてくれた。それは「ジャンケンの勝負での勝率は33.3%よりも減るかもしれないが、進める歩数が相手より多くなるような手の出し方だ」というものだった。なるほど。たとえば、グーで勝っても3歩しか進めないが、チョキやパーで勝てば6歩進めるから、チョキやパーを多く出すようにすれば、ジャンケンでは負ける確率が増えるかもしれないが、進む歩数は多くなるかも、ということは言えるかもしれない。
そこで、相手が片田法“グー、チョキ、パーを3分の1ずつランダムに出す(g、c、p)”という戦略を取っていると仮定して、こちらは、“グー、チョキ、チョキ、パーを4分の1ずつランダムに出す(G、C、C、P)”という戦略を取ってみることにしてみよう。それが図3である。
|
|
すると、総勝負数は3×4=12通りで、自分の総得点は21点、相手の総得点は18点となった。おっと、差がついた! ただし、このときの勝ち負けの確率はどちらも33.3%で変化はない。ひと勝負あたりの平均得点を取ってみると、自分は21÷12=1.75点で、相手は18÷12=1.5点となっている。その差は0.25点で、4回ジャンケンをするごとに1歩の割合で、自分のほうが余分に進めるということがわかる。相手にとってみれば、勝ち負けではほぼ互角なのに、歩数ではどんどん離されていくという、不思議な現象が起きていることになる。
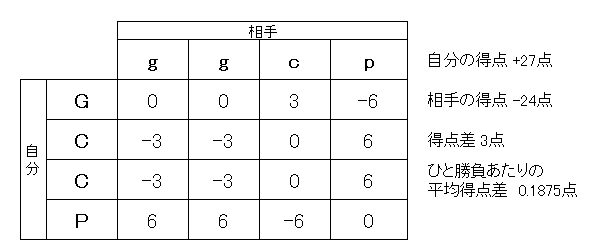
しかし相手もばかではないだろう。どうやら敵はチョキを多めに出している、ということに気が付くはずだ。そこで、相手の戦略もちょっと変えてみよう。つまり、チョキを多めに出す敵に対してグーを多めに出す戦略を取ってきたとする。このときの、相手“g、g、c、p”に対し自分が“G、C、C、P”を取ったときの結果が図4である。
|
|
だがしかし、このときも自分の総得点は27点、相手の総得点24点となり、依然として自分が多く進み続けていることがわかる。さらにおもしろいことに、勝ち負けの数を見てみると、全16通りの試合のうち、相手が勝つ場合が6通り、自分が勝つ場合が5通りと、相手のほうが多く勝っているのである。それにも係らず、自分のほうが多く進み続けられるのである。一応、ひと勝負あたりの平均得点も出しておこう。自分は27÷16=1.6875点、相手は24÷16=1.5点、差は0.1875点である。だから、この場合は5回ないしは6回の勝負ごとに、相手のほうが多く勝っているのにも係らず、じわりじわりと自分のほうが歩を進めていけることになる。
では、この“G、C、C、P”の戦略が最強かというとそうとは限らないだろう。もちろん、相手もまったく同じ“g、c、c、p”の戦略を取ってきたときには、どちらも総得点は24点ずつで対等な勝負となるし、相手がたとえば“g、c、c、c”の戦略を取ってきたときには、自分のほうが勝負数でも得点数でも負けるのである。
そこで、このように自分の出す手の割合を変えるという方向で、いったいどんな手を出したら、相手に得点数で勝つ確率が一番高くなるかを探っていくことにする。
2.数学的に表わせればなぁ
ということで、グリコケンの戦略と得点に関して数学的に表わせるよう考えてみた。
図2において、総得点をどのように計算してみたかというと、マトリックスの各行と各列を掛け合わせ、
Gg+Gc+GP+Cg+Cc+Cp+Pg+Pc+Pp ……式1
と置いたとき、自分の総得点なら
Gg=0, Gc=3, Gp=0, Cg=0, Cc=0, Cp=6, Pg=6, Pc=0, Pp=0
を代入して得られる得点、すなわち、
0+3+0+0+0+6+6+0+0=15点
が自分の得点であり、相手の得点は(マイナスで表わすと)
Gg=0, Gc=0, Gp=-6, Cg=-3, Cc=0, Cp=0, Pg=0, Pc=-6, Pp=0
を代入して、
0+0+(-6)+(-3)+0+0+0+(-6)+0=-15点
であるということである。このときの得点差は当然、
Gg=0, Gc=3, Gp=-6, Cg=-3, Cc=0, Cp=6, Pg=6, Pc=-6, Pp=0 ……式2
を代入して
0+3+(-6)+(-3)+0+6+6+(-6)+0=0点
である。
ところで式1を普通の数式とみて項ごとにまとめると
Gg+Gc+GP+Cg+Cc+Cp+Pg+Pc+Pp
=G(g+c+p)+C(g+c+p)+P(g+c+p)
=(G+C+P)(g+c+p) ……式3
と置くことができる。これはまさに
(G+C+P) 対 (g+c+p)
という戦略による勝負を表わしていることがわかる。たとえば図4の勝負は
(G+C+C+P)(g+g+c+p)
と書ける。このときの総得点の差は、途中計算は省くが、式2を代入して、3点となる。これはプラスの値なので、自分のほうが得点が多いということである。総得点差がマイナスになれば相手の得点のほうが多い。総勝負数は、自分の項の数×相手の項の数である。すなわち、(G+C+C+P)も(g+g+c+p)も4項目ずつあるので、
4×4=16通り
ということである。ひと勝負あたりの得失点差は、さきほどの3点をこの16通りで割って、
3÷16=0.1875
なので、確かに図4に関する考察結果と合致している。
ところで、
(G+C+C+P)=(G+2C+P)
(g+g+c+p)=(2g+c+p)
と書き換えることができ、これを掛け合わせた、
(G+2C+P)(2g+c+p)
=2Gg+Gc+Gp+4Cg+2Cc+2Cp+2Pg+Pc+Pp
に式2を代入するということは、結局、
(Gの個数)×(gの個数)×0 + (Gの個数)×(cの個数)×3
+ …… + (Pの個数)×(pの個数)×0
を求めているのと同じことだ。だから、G、C、P、g、c、pをそれぞれの手の個数とみなせば、式1の総得点差は、
0Gg+3Gc+(-6)Gp+(-3)Cg+0Cc+6Cp+6Pg+(-6)Pc+0Pp
を求めるのに等しい。勝負があいこのとき、すなわち得点が0のとき、たとえば上の式の第1項めの0×Gg=0となって消えるから、
0Gg+3Gc+(-6)Gp+(-3)Cg+0Cc+6Cp+6Pg+(-6)Pc+0Pp
=3G-6Gp-3Cg+6Cp+6Pg-6Pc
=3G(c-2p)+3C(2p-g)+6P(g-c) ……式4
となり、このときの答えがプラスなら自分の進める歩数が多く、マイナスなら相手の進める歩数が多いということになる。念のため図4の勝負について確かめておくと、G、C、P、g、c、pの個数、
(G,C,P)=(1,2,1)、(g,c,p)=(2,1,1)
すなわち、G=1, C=2, P=1, g=2, c=1, p=1
を式4に代入して
3(1-2)+6(2-2)+6(2-1)=3
となり、計算が正しいことがわかる。ついでにこのときの総勝負数は(自分の総個数)×(相手の総個数)なので、式3と同じ形なので紛らわしいが、
(G+C+P)(g+c+p)
=(1+2+1)(2+1+1)
=4×4
=16通り
である。
さて、式が立ったところで、G、C、P、g、c、pに次々と値を入れていって、答えがプラスになるかマイナスになるかを検証してみよう。それにはコンピューターの力を借りねばならないだろう。
3.コンピューターによるシミュレーション
だが、その前に少し考えておかなければならないことがある。
たとえば、自分がGしか出さないという戦略は考慮に値するだろうか。もちろん、値しないだろう。戦略がミエミエだからである。同様に、たとえば(G,C,P)=(2,1,0)、(G,C,P=(0,2,3)など2つしか手を出さない場合もすぐに戦略が相手にバレてしまう。後者の場合であれば、Cを2回、Pを3回の割合で出すということなのだが、どんなにランダムに出したところで、相手には「ははぁ、敵はCとPしか出さないな」ということがすぐにわかってしまう。つまり、相手はcさえ出しておけば勝つかあいこしかなく、必ず得点できるという戦略を取られてしまうからである。これは、G、C、Pのうちに、0(ゼロ)のある勝負は考慮に値しない、ということである。ただ、そうは言っても、相手はそのような戦略を取ってくるかもしれないから、相手の取りうる戦略としてはg、c、pの中に0(ゼロ)があるというのを認めておくことにする。先ほど図4の戦略が最強かどうかを考察したときに、自分の“G、C、C、P”に対し相手が“g、c、c、c”を取ったら、勝負数でも得点数でも負けてしまうと論じたことを思い出してほしい。
さて、そんなこんなで、自分が4つの手順の繰り返し、すなわち(G,C,P)=(2,1,1)、(1,2,1)、(1,1,2)を取ったときに、相手も最大で4つの手順の繰り返し戦略を取ったと仮定したときの勝負結果が図5の表である。
若干の説明を加えねばならない。まず、おさらいとして(G,C,P)=(2,1,1)は、この順番で
グー、グー、チョキ、パー、グー、グー、チョキ、パー、…
と繰り返して手を出すということではなく、この割合でランダムに出すということを、もう一度確認しておく。また、相手の出す手として、たとえば(g,c,p)=(4,0,0)というものもありうるが、これはグーしか出さないということだから(g,c,p)=(1,0,0)に等しく、重複するので省いてある。同様に(g,c,p)=(2,2,0)なども(g,c,p)=(1,1,0)に等しいので省いてある。表中に現われている数字は、式4を計算した総得点差を総勝負数で割ったものである。すなわち、ひと勝負あたりに進める歩数だ。くどいようだが、これがプラスなら自分の進める歩数が多く、マイナスなら相手の進める歩数が多い。
これを見ると、どの戦略をとっても“必ず勝てる”つまり、相手の戦略によらずすべてがプラスとなる自分の戦略は無いことがわかる。しかし、一番右に戦略ごとの平均を出しているので、それを見ると、
(G,C,P)=(2,1,1) のとき、平均得点差 -0.25
(G,C,P)=(1,2,1) のとき、平均得点差 0.25
(G,C,P)=(1,1,2) のとき、平均得点差 0
となっており、(G,C,P)=(1,2,1)という戦略を取ったとき、ひと勝負あたりの進める歩数が最も多いことがわかる。
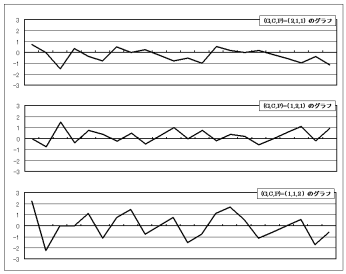
数字ではわかりにくいので、これをグラフにしてみたものが図6である。
グラフからわかるのは、
(G,C,P)=(2,1,1) の場合、値がマイナスとなるほうが多く、しかもその幅(絶対値)がプラスの幅に比べて大きい
(G,C,P)=(1,2,1) の場合、値がプラスとなるほうが多く、プラス幅のほうがマイナス幅より大きい
(G,C,P)=(1,1,2) の場合、値はプラスとなるほうが多いようだが、幅がプラス、マイナスともに大きい
ということである。つまり、(G,C,P)=(2,1,1) は戦略としてありえず、(G,C,P)=(1,1,2)はマイナス幅も大きいことから勝負としては危険が大きくギャンブル性が高い。そして(G,C,P)=(1,2,1)はプラス幅が小さいため、コツコツと歩数をかせいでいく戦略である。こうして見ても、やはり(G,C,P)=(1,2,1)すなわち“G、C、C、P”はかなりいい戦略なのだ。
さて、実は私は同様の計算をさらに広げ、10個の手順の繰り返しの場合までやってみた。まぁ、10手順の繰り返しとなると、さすがに覚えきれなくて、「あれ、次に何を出せばいいんだっけ?」となってしまうので、実用上は十分な計算精度であると言えるだろう。
さすがに、計算結果の表とグラフは、ここに載せるには大きすぎてしまうので省略するが、結果としては4つの手順の繰り返しと同じような傾向が出ることとなった。敵のすべての戦略に対し、必ず勝てる自分の戦略も存在しないことがわかった。こちらがどんな戦略を取ろうと、相手がそれを見破り、的確に対処してきたら、苦しい戦いとなるだろう。だが、相手の多くの戦略において勝てる自分の戦略なら挙げることができる。
|
|
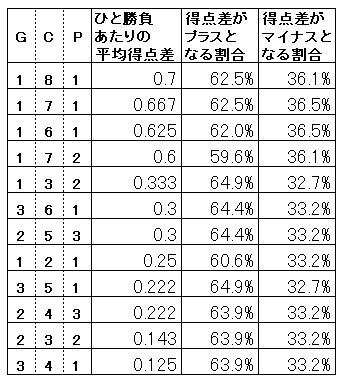
式4において、総得点差が、マイナスとなるのが約32.7%、プラスになるのが約64.9%という高い得点率をほこる戦略が2つあった。それは、(G,C,P)=(1,3,2)のときと、(3,5,1)のときだ。
また、総得点差が最も大きくなったものは(G,C,P)=(1,8,1)のときで、そのときの総得点差は0.7となった。そのほか、スコアの高い戦略を図7に記しておく。軽く解説しておくと、(G,C,P)=(1,8,1)は平均の得点差は0.7と高いが、得点差がマイナスとなる割合もやや高い。つまり、うまく勝てればたくさん進むことができるが、相手の戦略によっては相手に進まれてしまう確率も高いということだ。上でも述べたように、(G,C,P)=(1,3,2)と(3.5.1)のときは、プラスとなる割合が高く、マイナスとなる割合も低くて非常に優秀だが、平均得点差は0.22〜0.33とそれほど高くないので、進み方は遅いものになるだろう。さきほど4手順のときによい成績だった、(G,C,P)=(1,2,1)は、この中では見劣りしてしまう。また、図7には上げていないが、(G,C,P)=(8,1,1)は最悪で、平均得点差が、-0.7で、得点差がプラスとなる割合はわずか36%、マイナスとなるのは62.5%もある。
結.チョキを多く出せ
グリコケンにも、勝負に勝つ確率が最も高くなる方法があることがわかった。ただし、実際の勝負では、正確な割合でグー、チョキ、パーを出すことは難しいだろう。そこで、その方法を大ざっぱに言えば「チョキを多めに出す」ということになるだろう。そうすれば、ジャンケンには相手のほうが多く勝つかもしれないが、進める歩数はこちらのほうが多くなるのである。また、最悪なのはグーを多めに出しちゃうことで、パーはややひかえめに出しておくのがいいだろう。
どうだ、片田君、こんなもんじゃないだろうか(読んでないと思うけど)。
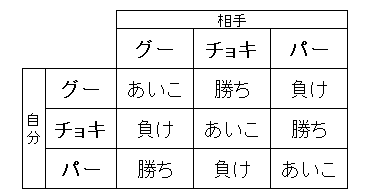 図1 ジャンケンの勝負マトリックス
図1 ジャンケンの勝負マトリックス